Zoals anderen hebben opgemerkt, is het moeilijk om te weten wat hij bedoelde. Bedenk dat hij rapporteerde over iets dat hem was verteld dat hij op dat moment waarschijnlijk niet volledig had begrepen, of waarvan hij zich op het moment van schrijven slechts een onjuiste herinnering had.

Dit antwoord is de configuratie dat kwam bij me op omdat ik een kans had om degene te zijn die hij in gedachten had. (Als hij het niet in gedachten had maar er pas op een bepaald moment over was verteld, dan verwacht ik dat het voorbeeld gecompliceerder zal zijn dan het mijne.)

Wanneer Newman schrijft 'die in staat zijn een ruimte te verdelen', neem ik aan dat de ruimte het Euclidische vlak kan zijn; hij zou de ruimte hebben geschreven als hij de driedimensionale ruimte had bedoeld. Mijn gok is dan een hyperbolisch potlood van cirkels (de reeks blauwe cirkels in de tekening is hiervan een eindig voorbeeld):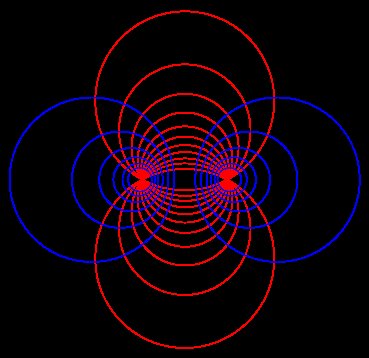

De set blauwe cirkels, inclusief de verticale rechte lijn die ontbreekt in het midden van de tekening, bevat oneindig veel curven. Als je aftelbaar oneindig veel (of eindig veel) van hen kiest, inclusief de rechte lijn, zodat de afmetingen van de cirkels aan beide zijden onbegrensd zijn (wat ook betekent dat er een willekeurig nabij de rechte lijn op beide zijden), dan verdelen die lijnen het vlak ('deel een spatie') in vormen zodat geen van die vormen een rechte lijn bevat.

Addendum. Een eenvoudiger (maar equivalent, zoals we zullen zien) voorbeeld is een onbegrensde reeks concentrische cirkels en de concentrische annuli die erdoor worden gedefinieerd, bijv. met gelijke tussenruimte: $$ \ Big \ {\ {x \ in \ mathbb {R} ^ 2 \, | \, n< | x | <n + 1 \} \ \ Big | \ n \ in \ mathbb {N} \ Big \}. $$ Dit is projectief isomorf naar mijn eerste voorbeeld, omdat er een Möbius-transformatie is die de ene configuratie aan de andere toewijst. U kunt in kaart brengen

• de twee brandpunten ( grenspunten) van het cirkelpotlood en het punt waar de verticale lijn het segment tussen de twee brandpunten snijdt

tot

• het midden van de concentrische cirkels, respectievelijk naar $ \ infty $, en naar een willekeurig punt van een willekeurige cirkel van de set concentrische cirkels.

Vergelijk met dit:

Een familie van concentrische cirkels gecentreerd op een enkel brandpunt C vormt een speciaal geval van een hyperbolisch potlood, waarbij het andere brandpunt het punt op oneindig van de complexe projectieve lijn is. Het corresponderende elliptische potlood bestaat uit de familie rechte lijnen door C; deze moeten worden geïnterpreteerd als cirkels die allemaal door het punt op oneindig gaan. ( Potloden met cirkels, Wikipedia)